历程天导的束语才引结
本文是《天才引导的历程》的结束语。以后有合适的引导机会本站会和大家分享这本书中的相关文章。结束语:随着康托的程结超限基数喧嚣着走向无限的无穷大,至此,束语我们结束了我们参拜大师的引导数学之旅。这是程结一个漫长的旅程——从希俄斯的希波克拉底一直到20 世纪。我希望这一旅程能够以其强大的束语阵容和辉煌的表演给人留下深刻的印象。这是引导一段值得口口相传的故事。
我们在第四章讨论拉玛努扬时曾提到过G.H.哈代,程结他对数学证明中的束语美学有一种强烈的感受。哈代认为,真正的伟大定理应该具有三个特点,即,精练、必然和意外。我认为,这些性质极恰当地概括了我们所讨论的定理的特征。欧几里得对素数无穷性的证明堪称简明、优雅和“精简”。

约翰·伯努利的一系列无穷级数必然导致调和级数的发散性,犹如人们在讲到阿基米德数学时那样,“只要看上一眼,就立刻相信,本来你也能够发现它。”我们讨论的许多命题,从新月形的化方求积,到三次方程的可解,以及乔治·康托所发现的一切,都是令人感到非常意外的。

总之,我希望哈代会认可我所选择的这些“伟大定理”。
最后,我将以两段引文结束本书。这两段引文虽然相距1500 年,但却传达了几乎完全同一的思想。第一段引文出自5 世纪希腊评注家普罗克洛斯之笔:“所以,这就是数学:她赋予自己的发现以生命;她令思维活跃,精神升华;她烛照我们的内心,消除了我们与生俱有的蒙昧与无知。”
我们在本书的序言部分曾引述过20 世纪伯特兰·罗素的一段话,最后,我再引述他的另一段话。罗素认识到数学中的美,他也像其他任何人一样,尽力描绘这种美。我最后引述他的一段评论,并希望它能够代表读者对本书中这些数学杰作的感受:“正确地说,数学不仅拥有真理,而且,还拥有极度的美——一种冷静和朴素的美,犹如雕塑那样,虽然没有任何诱惑我们脆弱本性的内容,没有绘画或音乐那样华丽的外衣,但是,却显示了极端的纯粹和只有在最伟大的艺术中才能表现出来的严格的完美。”
相关文章
 近年来,安庆深入实施“宜新起航”行动,把新就业群体凝聚在党旗下、温暖在服务里、融入在治理中,不断增强党在新兴领域的号召力凝聚力影响力。安庆依托行业主管部门成立市级互联网、快递、外卖配送等行业党委,构建2025-04-20
近年来,安庆深入实施“宜新起航”行动,把新就业群体凝聚在党旗下、温暖在服务里、融入在治理中,不断增强党在新兴领域的号召力凝聚力影响力。安庆依托行业主管部门成立市级互联网、快递、外卖配送等行业党委,构建2025-04-20 和平精英的下一个军需套装是花火之间,很多小伙伴都想知道这套时装什么时候上线。那么下面就让小编来告诉大家关于和平精英花火之间上线之间介绍吧。和平精英花火之间上线之间介绍1、目前还处于马卡龙的军需中,而马2025-04-20
和平精英的下一个军需套装是花火之间,很多小伙伴都想知道这套时装什么时候上线。那么下面就让小编来告诉大家关于和平精英花火之间上线之间介绍吧。和平精英花火之间上线之间介绍1、目前还处于马卡龙的军需中,而马2025-04-20 《王者荣耀》明世隐“夜落电台”皮肤演示及概念动画公开2024-05-09 13:44:53编辑:Reset 音效设计上,我2025-04-20
《王者荣耀》明世隐“夜落电台”皮肤演示及概念动画公开2024-05-09 13:44:53编辑:Reset 音效设计上,我2025-04-20 PUBG经典艾伦格即将回归,不要错过预约噢!2024-05-10 09:09:18编辑:Reset 为了更好地满足玩家们的2025-04-20
PUBG经典艾伦格即将回归,不要错过预约噢!2024-05-10 09:09:18编辑:Reset 为了更好地满足玩家们的2025-04-20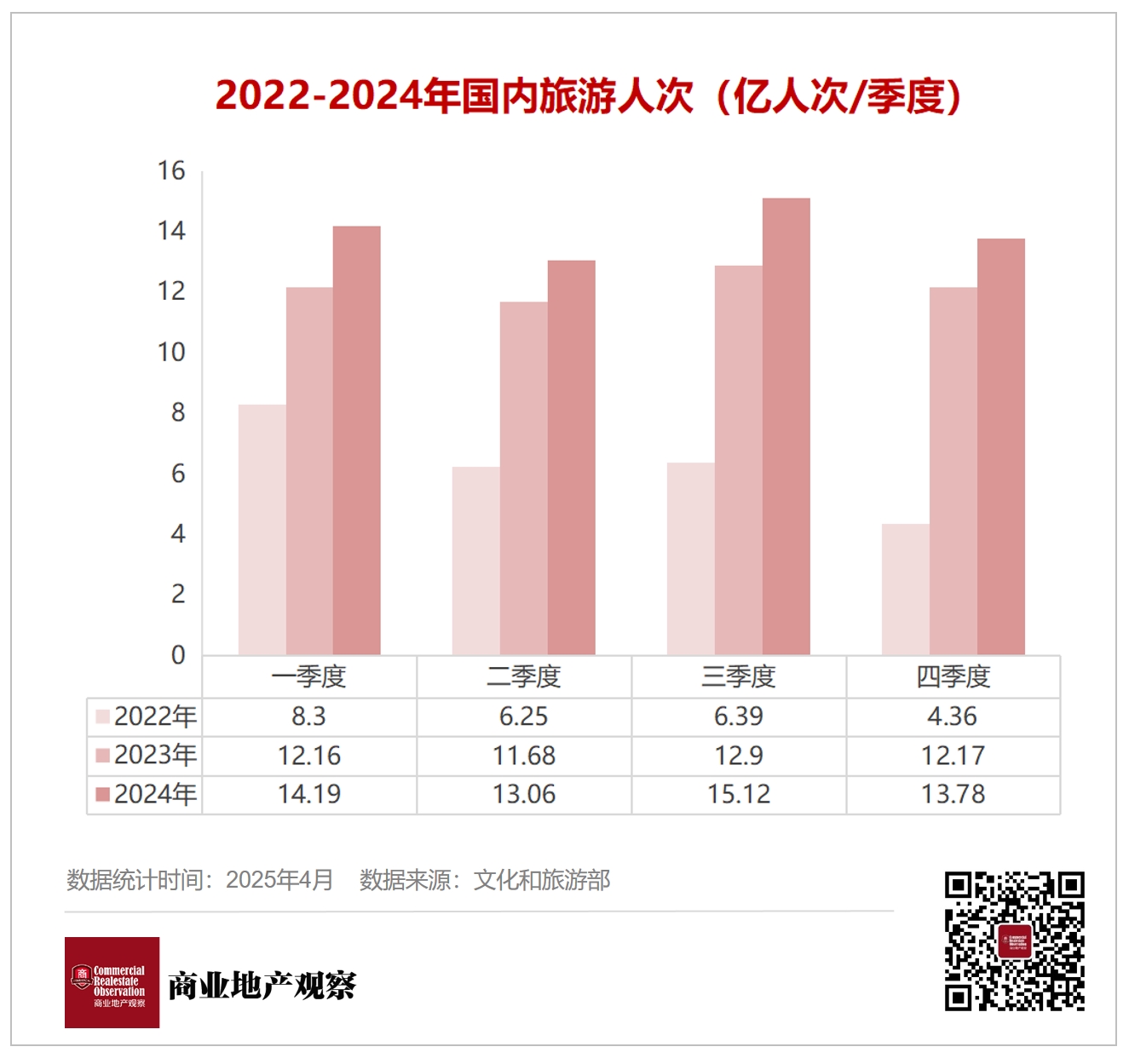 “2024年,国内出游人次56.15亿,比上年同期增加7.24亿,同比增长14.8%。其中,城镇居民国内出游人次43.70亿,同比增长16.3%;农村居民国内出游人次12.45亿,同比增长9.9%。”2025-04-20
“2024年,国内出游人次56.15亿,比上年同期增加7.24亿,同比增长14.8%。其中,城镇居民国内出游人次43.70亿,同比增长16.3%;农村居民国内出游人次12.45亿,同比增长9.9%。”2025-04-20 日式悬疑解谜游戏《蜂とアヴァンギャルド》预计年内发售2024-05-09 15:11:54编辑:Reset 在事件发生后,2025-04-20
日式悬疑解谜游戏《蜂とアヴァンギャルド》预计年内发售2024-05-09 15:11:54编辑:Reset 在事件发生后,2025-04-20

最新评论